Objectives:
To develop and validate a theoretical/numerical model describing formation of nanoparticle assemblies and to apply this model to formation of supraparticles and to formation of conductive printed circuits
Expected Results:
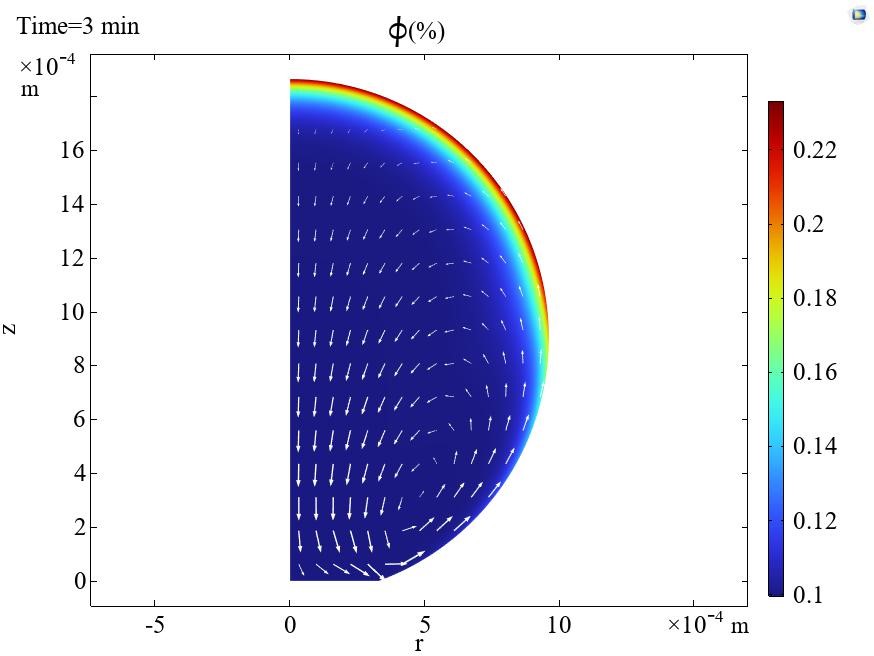
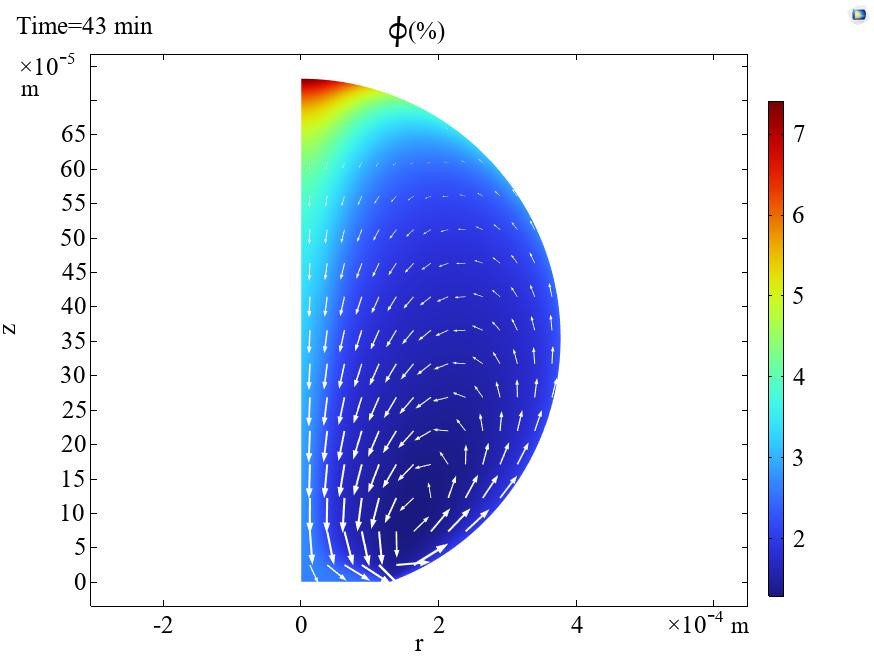
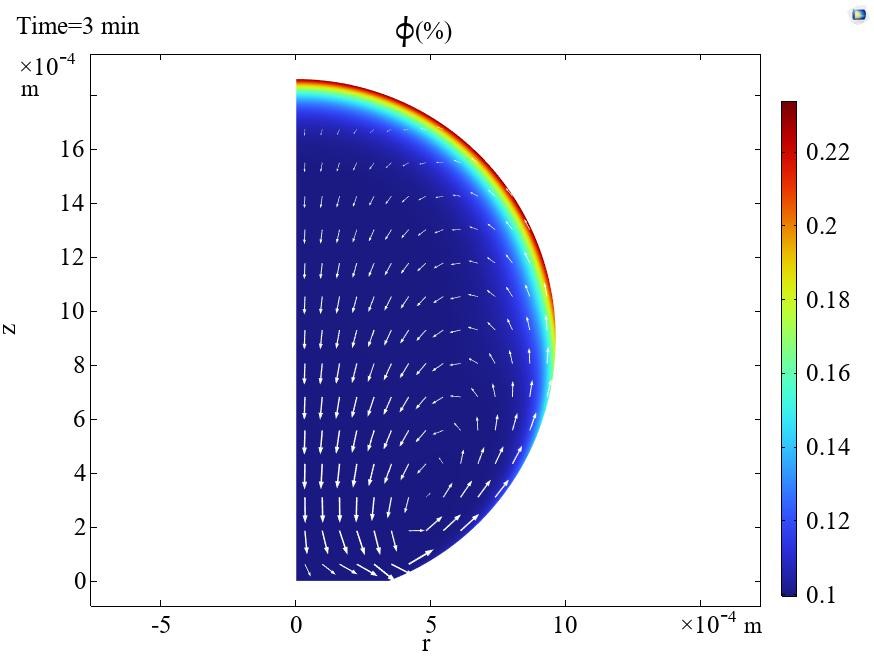
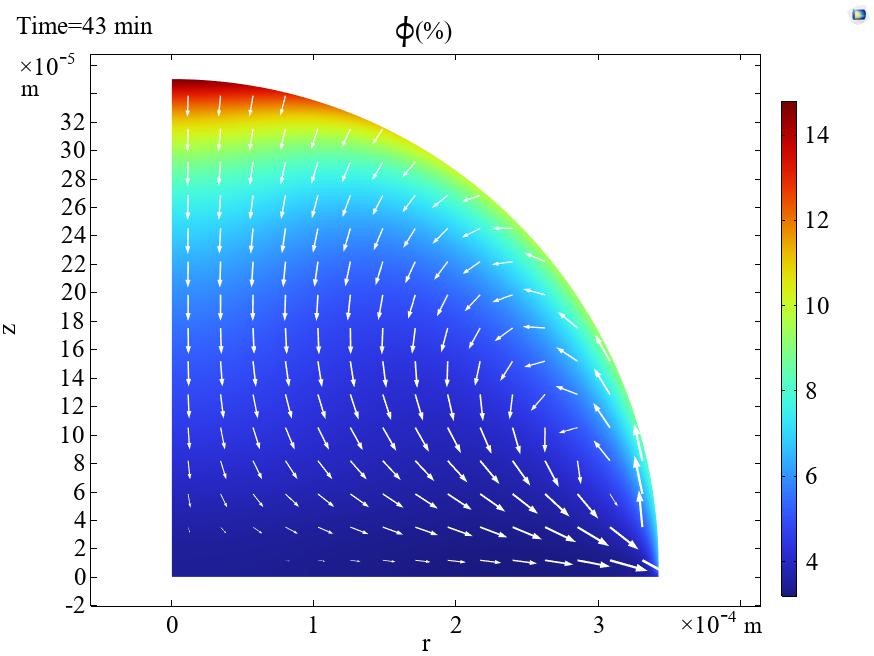
– Theoretical model and computer code describing flow and assembly of nanoparticles on substrates on the basis of colloidal nanoparticle interaction and nanoparticles dynamics model (WP1), interfacial flows model (WP2) and taking into account solvent evaporation;
– simulation of self-assembly of particles during coalescence and evaporation of two nanosuspension drops on a superoleophobic substrate (MPIP);
– simulation of formation of assemblies by evaporation of printed conductive inks/pastes (ICSC).
- The effect of diffusion coefficient on particles distribution during evaporation of drops deposited on superhydrophobic and parahydrophobic substrates
Introduction
The significance of nanofluid droplet evaporation is evident in its diverse applications, such as printing, coating, and supraparticle formation. Although both superhydrophobic and para-hydrophobic surfaces display high water contact angles, it’s important to note that the latter exhibits significantly higher contact angle hysteresis compared to the former. Simulating how nanoparticles are distributed within sessile droplets holds the potential for precise predictions regarding nanofluid drying and eventual deposition. It’s worth highlighting that the influence of the chosen diffusion coefficient model on nanoparticle dynamics has received limited attention in research so far.Aim
Our objective is to develop a novel Computational Fluid Dynamics (CFD) framework using COMSOL Multiphysics to predict the influence of surface wettability and the solute diffusion model on the evaporation behavior of nanoparticle-laden droplets.Diffusion Coefficient
Here we have applied the Stokes–Einstein equation, whose equation has been shown below:
D=kB ×T/(6πμrp)
Findings
CCA case
CCR case
